9 min read
How can you pick a sample that’s truly random and representative of the participant population? Simple random sampling is the sampling method that makes this easy. Learn how it works in our ultimate guide.
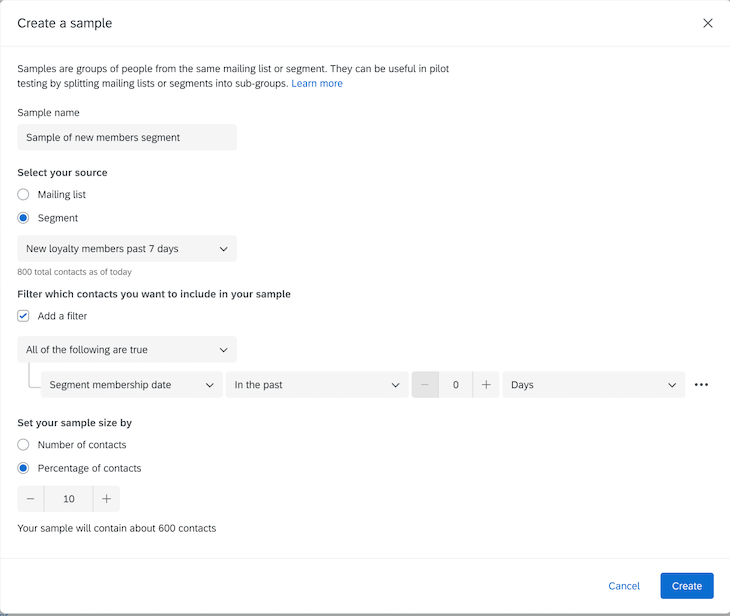
Simple random sampling selects a smaller group (the sample) from a larger group of the total number of participants (the population). It’s one of the simplest systematic sampling methods used to gain a random sample.
The technique relies on using a selection method that provides each participant with an equal chance of being selected, giving each participant the same probability of being selected. Since the selection process is based on probability and random selection, the end smaller sample is more likely to be representative of the total population and free from researcher bias. This method is also called a method of chances. Simple random sampling is one of the four probability sampling techniques: Simple random sampling, systematic sampling, stratified sampling, and cluster sampling. Start your free 30-day trial of XM for Strategy & Research today
Creating a simple random sampling size is easy with Qualtrics XM. Build your own in-house panel with rich profiles of your customers and prospects.

Simple random sampling is normally used where there is little known about the population of participants. Researchers also need to make sure they have a method for getting in touch with each participant to enable a true population size to work from. This leads to a number of advantages and disadvantages to consider.
This sampling technique can provide some great benefits.
A lottery is a good example of simple random sampling at work. You select your set of numbers, buy a ticket, and hope your numbers match the randomly selected lotto balls. The players with matching numbers are the winners, who represent a small proportion of winning participants from the total number of players.
Other selection methods used include anonymizing the population – e.g. by assigning each item or person in the population a number – and then picking numbers at random.
Researchers can use a simpler version of this by placing all the participants’ names in a hat and selecting names to form the smaller sample.
The three other types of probability sampling techniques have some clear similarities and differences to simple random sampling:
Systematic sampling, or systematic clustering, is a sampling method based on interval sampling – selecting participants at fixed intervals.
All participants are assigned a number. A random starting point is decided to choose the first participant. A defined interval number is chosen based on the total sample size needed from the population, which is applied to every nth participant after the first participant.
For example, the researcher randomly selects the 5th person in the population. An interval number of 3 is chosen, so the sample is populated with the 8th, 11th, 14th, 17th, 20th, (and so on) participants after the first selection.
Since the starting point of the first participant is random, the selection of the rest of the sample is considered to be random.
Simple random sampling differs from systematic sampling as there is no defined starting point. This means that selections could be from anywhere across the population and possible clusters may arise.
Stratified sampling splits a population into predefined groups, or strata, based on differences between shared characteristics – e.g. race, gender, nationality. Random sampling occurs within each of these groups.
This sampling technique is often used when researchers are aware of subdivisions within a population that need to be accounted for in the research – e.g. research on gender split in wages requires a distinction between female and male participants in the samples.
Simple random sampling differs from stratified sampling as the selection occurs from the total population, regardless of shared characteristics. Where researchers apply their own reasoning for stratifying the population, leading to potential bias, there is no input from researchers in simple random sampling.
There are two forms of cluster sampling: one-stage and two-stage.
One-stage cluster sampling first creates groups, or clusters, from the population of participants that represent the total population. These groups are based on comparable groupings that exist – e.g. zip codes, schools, or cities.
The clusters are randomly selected, and then sampling occurs within these selected clusters. There can be many clusters and these are mutually exclusive, so participants don’t overlap between the groups.
Two-stage cluster sampling first randomly selects the cluster, then the participants are randomly selected from within that cluster.
Simple random sampling differs from both cluster sampling types as the selection of the sample occurs from the total population, not the randomly selected cluster that represents the total population.
In this way, simple random sampling can provide a wider representation of the population, while cluster sampling can only provide a snapshot of the population from within a cluster.
Where sample sizes and the participant population are large, manual methods for selection aren’t feasible with the available time and resources.
This is where computer-aided methods are needed to help to carry out a random selection process – e.g. using a spreadsheet’s random number function, using random number tables, or a random number generator.
Let’s take an example in practice. A company wants to sell its bread brand in a new market area. They know little about the population. The population is made up of 15,000 people and a sample size of 10% (1,500) is required. Using this example, here is how this looks as a formula:
Sample size (S) = 1,500
The total population (P) = 15,000
The probability of being included in the sample is: (S ÷ P) x 100%
E.g. = (1,500 ÷ 15,000) x 100% = 10%
One way of randomly selecting numbers is to use a random number table (visual below). This places the total population’s sequential numbers from left to right in a table of N number of rows and columns.
To randomly select numbers, researchers will select certain rows or columns for the sample group.
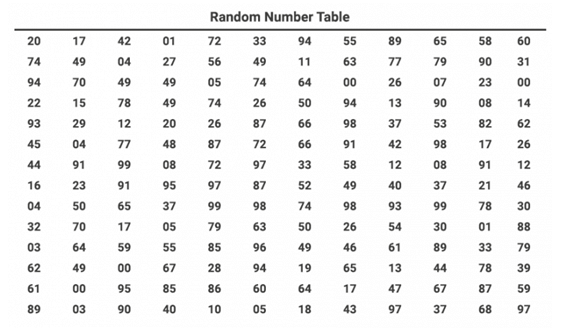
As sourced from Statistical Aid
Microsoft Office’s Excel spreadsheet application has a formula that can help you generate a random number. This is:
It provides a random number between 1 and 0.
For random numbers from the total population (for example, a population of 1000 participants), the formula is updated to:
=INT(1000*RAND())+1
Simply copy and paste the formula into cells until you get to the desired sample size – if you need a sample size of 25, you must paste this formula into 25 cells. The returned numbers between 1 and 1000 will indicate the participant’s ID numbers that make up the sample.
Start your free 30-day trial of XM for Strategy & Research today